2022年国家公务员考试行测真题（数量关系与资料分析部分）

2022年国家公务员考试行测真题（数量关系与资料分析部分）

数量关系
　　61.某企业职工筹款给甲村学龄儿童购买学习用具，如按100元/人的标准执行则资金剩余550元，如按120元/人的标准执行则还需筹集630元。现额外筹集2510元，且最终按80元/人的标准，正好能给甲、乙两村的学龄儿童购买学习用具。问乙村学龄儿童有多少人：
　　a．50　　b．53　　c．56　　d．59

【答案】b。解析：简单基础应用题。设甲村学龄儿童为x人，由题意得，100x+550=120x-630，解得x=59人，则原来筹款资金为100×59+550=6450元。现额外筹集2510元，则此时共有6450+2510=8960元。根据“80元/人的标准”，可得甲乙两村的学龄儿童人数有：8960÷80=112人，则乙村学龄儿童有112-59=53人，答案选b。

　　62.甲、乙、丙、丁、戊5名职工参加党史知识测验，每人得分均不相同。甲和乙的平均分比丙多2分，丁和戊的平均分比丁多5分，甲、乙的平均分比丙、丁、戊的平均分多3分。问丙、丁、戊三人得分的排序为：
　　a．丙>丁>戊　　b．丙>戊>丁　　c．丁>丙>戊　　d．戊>丙>丁

【答案】d。解析：平均数问题。由“甲和乙的平均分比丙多2分”得，甲+乙=2（丙+2），即：甲+乙=2丙+4①；由“丁和戊的平均分比丁多5分”得，丁+戊=2（丁+5），即：戊=丁+10②；由“甲、乙的平均分比丙、丁、戊的平均分多3分”得，

③；把①代入③整理得，丙=丁+6.5④，则戊=丁+10>丙=丁+6.5>丁，答案选d。　　

63.企业列出500万元设备采购预算，如用于购买x台进口设备，最后剩余20万元。经董事会研究后，决定购买质量更高的同类国产设备，单价仅为进口设备的75%。当前预算可购买x+3台，最后剩余5万元。问国产设备的单价在以下哪个范围内：
　　a．不到30万元/台　　 b．30—40万元/台之间　　

c．40—50万元/台之间　　d．50万元/台以上

【答案】c。解析：基础应用题。由题意知，每台进口设备单价为：（500-20）÷x=480/x万元。若购买国产设备，单价为进口设备的75%，则国产设备的单价为480/x ×75%=360/x。当前预算可购买国产设备x+3台，最后剩下5万元，则得360/x (x+3)=500-5，解得x=8.则共购买国产设备为8+3=11台，花费495万元，其单价为495÷11=45万元，在c项范围，答案选c。

　　64.甲和乙两个乡村图书室共有5000本藏书，其中甲图书室的藏书比乙图书室多3x本。现从甲图书室中取出150本书放入乙图书室后，甲图书室的藏书仍比乙图书室多2x本。问甲图书室原有图书多少本：
　　a．2500　　b．2750　　c．2950　　d．3500

【答案】c。解析：基础应用题。设甲图书馆原有藏书y本，则乙图书室藏书为y-3x本，由题意得，y+y-3x=5000①；甲图书室中取出150本放入乙图书室，则甲有y-150本，乙有y-3x+150本，由题意得，（y-150)-(y-3x+150)=2x②，由②解得，x=300，代入①式得，解得y=2950，即甲图书室原有图书2950本，答案选c。

　　65.李某骑车从甲地出发前往乙地，出发时的速度为15千米/小时，此后均匀加速，骑行25%的路程后速度达到21千米/小时。剩余路段保持此速度骑行，总路程前半段比后半段多用时3分钟。问甲、乙两地之间的距离在以下哪个范围内：
　　a．不到23千米　　 b．在23—24千米之间　　

1. 在24—25千米之间　　d．超过25千米

【答案】d。解析：行程问题.匀加速运动。设总行程为4s，则总行程前半段为2s千米，后半段为2s千米。总行程前25%的路程为匀加速运动，初速度为15千米/时，末速度为21千米/时，则匀加速运动平均速度为

。由“总路程前半段比后半段多用时3分钟”得，

，解得，s=6.3，故全程为4s=4×6.3=25.2千米，答案选d。

注：匀加速运动：加速度为a，初速度为v0，末速度为vt，位移为s，则相关公式：

1. 平均速度：； 末速度：；加速度：
2. 位移：

　　66.高校某专业70多名毕业生中，有96%在毕业后去西部省区支援国家建设。其中去偏远中小学支教的毕业生占该专业毕业生总数的20%，比任职大学生村官的毕业生少2人，比在西部地区参军入伍的毕业生多1人，其余的毕业生选择去国有企业西部边远岗位工作。问去国有企业西部边远岗位工作的毕业生有多少人：
　　a．32　　b．29　　c．26　　d．23

【答案】c。解析：整除性问题。由专业总人数的96%=24/25毕业后去西部支援，根据整除性知，总毕业人数25的倍数，则总毕业生人数为为75人。故去西部支援国家建设的毕业生有75×96%=72人，去偏远中小学支教的毕业生有75×20%=15人，去任职大学生村官的毕业生有15+2=17人，在西部参军入伍的毕业生有15-1=14人，则去国有企业西部边远岗位工作的毕业生有72-15-17-14=26人，答案选c。

　　67.某地引进新的杂交水稻品种，今年每亩稻谷产量比上年增加了20%，且由于口感改善，每斤稻谷的售价从1.5元提升到1.65元。以此计算，今年每亩稻谷的销售收入比上年高660元。问今年的稻谷亩产是多少斤：
　　a．2200　　b．1980　　c．1650　　d．1375

【答案】c。解析：比例计算问题。设去年每亩稻谷产量为x斤，则今年为（1+20%）x=1.2x斤。今年每亩稻谷销售收入比去年高660元，即1.65×1.2x-1.5x=660，解得 x=1375，则今年的稻谷亩产为1.2×1378=1650，答案选c。
　　68.甲地在丙地正西17千米，乙地在丙地正北8千米。张从甲地、李从乙地同时出发，分别向正东和正南方向匀速行走。两人速度均为整数千米/小时，且1小时后两人的直线距离为13千米，又经过3小时后两人均经过了丙地且直线距离为5千米。已知李的速度是张的60%，则张经过丙地的时间比李：
　　a．早不到10分钟　　b．早10分钟以上　c．晚不到10分钟　　d．晚10分钟以上

< p>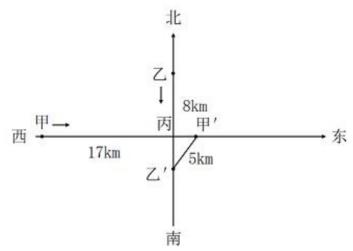

【答案】d。解析：方位几何与行程问题综合。如图所示，设张的速度为5m千米/小时，则李的速度为3m千米/小时。由题意可知，张、李两人1小时后直线距离为13千米，又经过3小时后直线距离为5千米，且此时均经过了丙地，即出发4小时后张李两人分别到达图示甲，、乙，处。则根据勾股定理得，（5m×4-17）2+（3m×4-8）2=52，因两人速度均为整数千米/时，则m=1时，符合题干所有要求。因此张到达丙地需要17/5小时，即3小时24分钟，李到达丙地需要8/3小时，即2小时40分钟，故张经过丙地的时间比李晚44分钟，答案选d。
　　69.某县通过发展旅游业来实现乡村振兴，引进了甲、乙、丙、丁、戊和己6名专家。其中甲、乙、丙是环境保护专家，丁、戊、己是旅游行业专家，甲、丁、戊熟悉社交媒体宣传。现要将6名专家平均分成2个小组，每个小组都要有环境保护专家、旅游行业专家和熟悉社交媒体宣传的人，问有多少种不同的分组方式：
　　a．12 　b．24　　c．4　　d．8

【答案】d。解析：排列组合问题。先将熟悉社交媒体宣传的3人分成两组，每组至少1从共有3种情况：①甲和丁戊两组；②甲丁和戊两组；③甲戊和丁两组。

①中：根据题意，己必须和甲一组甲组剩下1人由乙丙两个选一个，剩下自动与丁戊成一组，共

=2种方法；

②中：只要剩余3人选一个与甲丁组，剩余与戊自动对应一组，共有

=3种；

③中：与第二种情况同理，共有

=3种。总共有2+3+3=8种不同的分组方式，答案选d。
　　70.某水果种植特色镇创办水果加工厂，从去年年初开始通过电商平台销售桃汁、橙汁两种产品。从去年2月开始，每个月桃汁的销量都比上个月多5000盒，橙汁的销量都比上个月多2000盒。已知去年第一季度桃汁的总销量比橙汁少4.5万盒，则去年桃汁的销量比橙汁：
　　a．多不到5万盒　　b．少不到5万盒　　c．多5万盒以上　　d．少5万盒以上

【答案】b。解析：数列问题。设去年1月桃汁销量为x万盒，去年1月橙汁销量为y万盒，根据等差数列通项，则去年12月桃汁销量为：x+(12-1)×0.5=5.5+x万盒；去年12月橙汁销量为：y+(12-1)×0.2=2.2+y；

根据去年第一季度桃汁的总销量比橙汁少4.5万盒得，(3b+0.6)-(3a+1.5)=4.5，

解得，b-a=1.8万盒；

则去年桃汁总销量为：

万盒；

去年橙汁总销量为：

万盒；

故去年桃汁总销量比橙汁总销量12x+33-(12y+13.2)=12(x-y)+19.8=12×(-1.8)-19.8=-1.8万盒，即少1.8万盒，答案选b。
　　71.救灾部门紧急运送两批大米分给受灾群众。已知甲村人数是丙村的2倍，如果两批大米都给甲村，每人正好能分24斤；如果第一批大米分给乙村，每人正好能分12斤，第二批大米分给甲、乙、丙三个村，每人正好能分4斤。为尽量保障受灾群众的基本需求，现决定另运送一批面粉分给甲村，并将两批大米都分给乙、丙两村。问乙、丙两村平均每人分到的大米重量在以下哪个范围内：
　　a．不到14斤　　b．14～15斤之间　　c．15～16斤之间　　d．16斤以上

【答案】b。解析：简单平均数问题。设丙村有x人，乙村有y人，则甲村有2x人。根据两批大米的总重量不变得，24×24x=12y+4(2x+y+x)，解得，y=9/4x，故两批大米都分给乙、丙两村，平均每人分到的大米重量为：

，答案选b.

　　72.为降低碳排放，企业对生产设备进行改造，改造后日产量下降了10%，但每件产品的能耗成本下降了50%，其他成本和出厂价不变的情况下每天的利润提高10%。已知单件利润=出厂价-能耗成本-其他成本，且改造前产品的出厂价是单件利润的3倍，则改造前能耗成本为其他成本的：
　　a．不到1/4　　b．1/4~1/3之间　　c．1/3~1/2之间　　d．超过1/2

【答案】b。解析：利润问题。设改造前单件产品利润为x，出厂价为3x；单件产品能耗成本为y，其他成本为z。赋值改造前日产量为100，则改造后日产量为90。

根据改造前的单件产品利润得，3x-y-z=x，即2x-y=z①；

根据改造前后每天的利润得，90（3x-0.5y-z)=100x(1+10%)，整理得，16x-4.5y=9z②;

联合①②消除x得，3.5y=z，即

，改造前能耗成本为其他成本在1/4~1/3之间，答案选b.
　　73.一个圆柱体零件的高为1，其圆形底面上的内接正方形边长正好也为1。现将该圆柱体零件切割4次，得到棱长为1的正方体，则切去部分的总面积为：
　　a．(

+1)

+2　　b．

(

+2)　　c．2

(

-2)　　d．2

-2

【答案】a。解析：立体几何计算题。如图所示，

< p>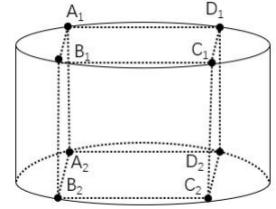

圆柱底面圆内接正方形边长为1，则正方形对角线为圆的直径，半径为

。沿着圆内接正方形的4条边垂直切割4次即得到棱长为1的正方体，且切去的4个部分完全相同，则切去部分表面积为：圆柱体的侧面面积、圆柱体的2个底面积扣除内接正方形的部分、正方体的4个侧面。

圆柱4个侧面积：4×1=4； 圆柱侧面积：

；

两个底面圆除去内接正方形面积：

；

s总=

，答案选a。

　　74.甲和乙两条效率相同的生产线从早上不同时间开始生产同一种产品，到中午12：00时分别正好生产了x件和y件。已知乙生产x件时，甲生产了54件；甲生产y件时，乙生产了1.5x件。如乙从9：00开始生产且12：00后两条生产线仍保持原有速度，问两条生产线生产的产品总量达到500件是在什么时候：
　　a．16：30之前　　 b．16：30～17：00之间　　

c．17：00～17：30之间　　d．17：30之后

【答案】d。解析：工程问题。根据甲乙两条生产线效率相同，故在甲、乙均开始生产后，两条件生产线生成产品数量的差值始终不变，则得，y-x=x-54=1.5x-y，解得，x=72，y=90。由由乙从9：00开始生产，到12：00时乙生产了3小时，生产了90件，则甲、乙的效率为90/3=30件/小时，甲、乙共生产了72+90=162件，则两条生产线生产的产品总量达到500件还需要（500-162）÷（30+30）=338÷60=

小时 ，即时间为17：38时，两条生产线的产品总量达到500件。

　　75.某种商品的定价为成本的1.5倍，如果在降价30元/件的基础上再打八折，则销售5件这种商品的利润比原价销售1件时多130元。问用以下哪种折扣销售时，1.5万元能买到的件数正好比原价销售时多4件：
　　a．先降价50元/件再打八折　　b．先打九折再降价50元/件
　　c．降价150元/件　　 d．打八五折

【答案】b。解析：利润问题。设该种商品每件成本为x元，则每件定价为1.5元。根据题意可列方程：5[(1.5x-30)×0.8-x]-(1.5x-x)=130，解得，x=500，即该种商品每件成本为500元，则每件定价为1.5×500=750元。按原价销售时，1.5万元可购买15000/750=20件，按选项折扣销售时，1.5万元需要购买20+4=24件，此时每件销价应为15000/24=625元。代入选项:

1. 折扣售价=（750-50）×0.8=560，不合；
2. 折扣售价=750×0.9-50=625元，符合，无需验证其他选项。答案选b.

2022年国考数量关系：

整体难度比往年降低，考得大多是常规基础题型，只是出现一个少考的均加速运动的行程问题。基础题难度较小的有8～9个，中度难度的综合分析题有4～5个，只有1～2个题型综合性强，难度稍大。多数题强调计算，要求计算快而准确。

1. 某单位办事大厅有3个相同的办事窗口，2天最多可以办理600笔业务，每个窗口办理单笔业务的用时均相同。现对该办事大厅进行流程优化，增设2个与以前相同的办事窗口，且每个办事窗口办理每笔业务的用时缩短到以前的。问优化后的办事大厅办理6000笔业务最少需要多少天？
   　　a、8　　b、10　　c、12　　d、15

【答案】a。解析：比例计算问题。每个窗口办理单笔业务的用时均相同，则1个窗口1天可以办理业务600÷3÷2=100笔，根据题意，增设2个窗口，且每个窗口办理每笔业务的用时缩短到以前的2/3，同一项业务，办理时间和办理效率成反比，则每笔业务办理的效率是原来的3/2，即优化后1个窗口1天可办理业务100×3/2=150笔。设优化后6000笔业务最少需要t天办理完成，则有6000=150×（3+2）t,解得，t=8，即最少需要8天，答案选a。

　　64、张和李2名社区工作者上门统计某小区内住户的新冠疫苗接种情况，两人各负责1栋住宅楼，每访问1户居民均需要5分钟。李因处理公文比张晚出发一段时间。已知14:00时两人共访问63户，15:00时张访问的户数是李的2倍。问李访问完50户居民是在什么时候？
　　a、16:30　　b、16:45　　c、17:00　　d、17:15

【答案】b。解析：基础和差倍比问题。两人每访问1户居民均需要5分钟，则1小时每人各访问12户，设14：00时，张已经访问了x户，则李访问了63-x户。根据题意得，

x+12=2(63-x+12)，解得，x=46,则李访问了63-46=17户，李到了15：00时共访问了17+12=29户，访问完50户则还需要访问50-29=21户，需要用时21×5=105分钟=1小时45分，即在16：45时访问完，答案选b。
68、某企业将5台不同的笔记本电脑和5台不同的平板电脑捐赠给甲、乙两所小学,每所学校分配5台电脑。如在所有可能的分配方式中随机选取一种，两所学校分得的平板电脑数量均不超过3台的概率为：

1. b、 c、 d.
   　　【答案】d。解析：概率问题。根据题意，甲、乙两所学校分配5台电脑的总数总数为：种；满足两所学校分得平板电脑数量均不超过3台的情况分类讨论如下：

①甲学校分得2台笔记本电脑、3台平板电脑，则乙学校分得3台笔记本电脑、2台平板电脑，情况数为：

种；

②甲学校分得3台笔记本电脑、2台平板电脑，则乙学校分得2台笔记本电脑、3台平板电脑，情况数为：

种；则所求概率为：

，答案选d。

　70、甲、乙等16人参加乒乓球淘汰赛,每轮对所有未被淘汰选手进行抽签分组两两比赛，胜者进入下一轮。已知除甲以外，其余任意两人比赛时双方胜率均为50%。甲对乙的胜率为0%，对其他14人的胜率均为100%。则甲夺冠的概率为：

1. b. c. d.

【答案】c。解析：概率与比赛问题问题。根据题意，甲若想夺冠，需进行四轮比赛且比赛中不能与乙同组比赛，正面讨论比较复杂，正难则反，考虑反面情况（甲乙同组比赛），分类讨论如下：

甲在第一轮与乙比赛：甲在第一轮碰到乙的概率为1/15，则淘汰概率为1/15；

甲在第二轮与乙比赛：甲、乙在第一轮均胜出的概率为

，甲在第二轮碰到乙的概率为1/7，则淘汰概率为：

；

甲在第三轮与乙比赛：甲、乙在第一轮胜出的概率为7/15,在第二轮均胜出的概率为

；甲在第三轮碰到乙的概率为1/3，则淘汰概率为

；

甲在第四轮与乙比赛，甲、乙在第一轮均胜出的概率为7/15，在第二轮均胜出的概率为3/7,第三轮均胜出的概率为

；甲在第四轮碰到乙的概率为1，则甲在第四轮淘汰的概率为

；

则甲获得冠军的概率为：1-（

，答案选c。

资料分析
　　暂缺（2022国考行测副省级）
　　116-120暂缺
　　2020年h省秋粮平均生存成本及同比增速

< p>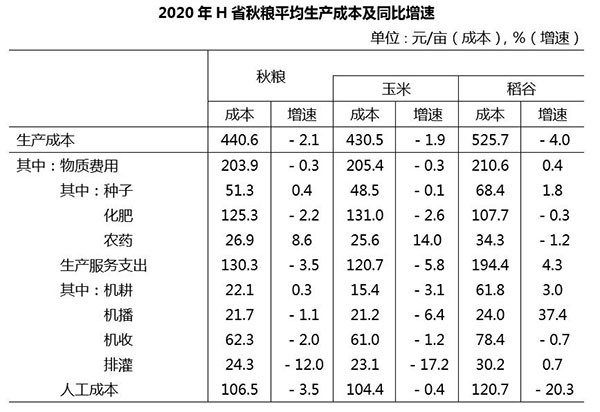

　　2020年，h省秋粮玉米和稻谷的市场平均交易价格分别为2.34元/公斤和2.74元/公斤，分别比上年上涨28.6%和8.7%。按此价格测算，2020年全省农户种植玉米、稻谷扣除成本前的产值分别为957.1元/亩、1520.7元/亩，分别比上年增长33.4%、8.9%。

121.2019年，h省秋粮稻谷的平均生产成本约为多少元/亩：
　　a．439　　b．450　　c．533　　d．548

【答案】d。解析：基期量计算。由表格得2019年h省秋粮稻谷的平均生产成本为：

元/亩，与d最接近。

122.将2020年h省秋粮机耕、机播、机收、排灌成本按同比增量从高到低的顺序排列，以下正确的是：
　　a．机收、排灌、机耕、机播　　b．机耕、机播、机收、排灌
　　c．机耕、机播、排灌、机收　　d．机收、排灌、机播、机耕

【答案】b。解析：增量比较大小问题。由表格知，

2020年h省秋粮机耕成本增量为：22.1×0.3%；机播成本增量：21.7×（-1.1%）；

机收成本增量：62.3×（-2%）；排灌成本增量：24.3×（-12.0%）；大小比较排序：机耕成本增量>机播成本增量>机收成本增量>排灌成本增量，答案选b。
123.2020年，h省秋粮玉米和稻谷的亩产与上年相比：
　　a．仅稻谷亩产高于上年水平　　b．仅玉米亩产高于上年水平

c.两者亩产均高于上年水平　　 d．两者亩产均低于上年水平

【答案】c。解析：比例的变化分析。由题意知，亩产=每亩产值/平均交易价格。由文字材料知，2020年，h省秋粮玉米和稻谷的市场平均交易价格分别比上年上涨28.6%和8.7；产值分别上涨33.4%和8.9%，根据比例变化规律，a>b，比例上升，即与上年相比均高于上年水平，答案选c。

1. 如种植收益=产值－生产成本，则2020年h省秋粮稻谷平均每亩的种植收益约是玉米的多少倍：
   　　a．1.9　　b．1.6　　c．0.7　　d．0.5

【答案】a。解析：现期倍数计算。由材料知，2020年h省秋粮玉米和稻谷的平均生产成本分别为430.5元/亩和525元/亩；产值分别为957.1和1520.7元/亩。根据种植收益=产值-生产成本，所求倍数为：

，答案选a。
125.2020年，h省农民老王在承包地中种植秋粮玉米，按全省平均生产成本估算，他在种子和农药上需要花费2000元。如亦按全省平均生产成本估算，他需要花费的人工成本在以下哪个范围内：
　　a．不到2000元　　 b．2000—2500元之间　　

c．2500—3000元之间　　d．超过3000元

【答案】c。解析：平均数计算。由表格知，2020年h省秋粮玉米种子的平均生产成本为48.5/亩，农药的平均生产成本为25.6元/亩，玉米的人工成本为104.4元/亩。老王在种子和农药上花费2000元，则老王承包土地的总亩数为2000÷（48.5+25.6）=2000/74.1亩，故他需要的人工成本为：

元，答案选c。
　　

暂缺（2022国考行测副省级）
　　126-130暂缺
　　2020年12月,c市天然气用量为9.67亿立方米,同比增长11.66%。从供应结构看：中石油供应7.22亿立方米,同比增长7.44%;中石化供应2.45亿立方米,同比增长26.29%。从用气结构看：民用气为3.98亿立方米,同比增长16.72%；cng用气0.64亿立方米,同比下降7.25%;工业用气5.05亿立方米,同比增长10.75%。
　　2020年,c市天然气用量为107.47亿立方米,同比增长3.83%。其中,中石油供应73.96亿立方米,同比增长1.72%;中石化供应33.51亿立方米,同比增长8.8%。从用气结构看:民用气为33.75亿立方米,同比増长5.4%;cng用气6.99亿立方米,同比下降13.92%；工业用气66.73亿立方米,同比增长5.3%。
　　2021年2月,c市天然气用量为9.31亿立方米,同比增长21.38%。从供应结构看:中石油供应6.7亿立方米,同比增长25.23%；中石化供应2.61亿立方米,同比增长12.5%。从用气结构看:民用气为3.56亿立方米,同比增长16.34%;cng用气0.52亿立方米,同比增长205.88%;工业用气5.23亿立方米,同比增长17.79%。
　　2021年1—2月,c市天然气用量为19.21亿立方米,同比增长12.8%。其中,中石油供应14.23亿立方米,同比增长18.88%;中石化供应4.98亿立方米,同比下降1.58%。从用气结构看:民用气为7.78亿立方米,同比增长12.75%;cng用气1.14亿立方米,同比增长44.3%；工业用气10.29亿立方米,同比增长10.17%。
131.2021年1月，c市天然气用量比上月：
　　a．增加了0.2亿立方米以上　　b．减少了不到0.2亿立方米
　　c．减少了0.2亿立方米以上　　d．增加了不到0.2亿立方米

【答案】a。解析：简单增量计算。由材料知，2021年2月,c市天然气用量为9.31亿立方米；2021年1—2月,c市天然气用量为19.21亿立方米；2020年12月,c市天然气用量为9.67亿立方米；2021年1月，c市天然气用量为：19.21-9.31=9.9亿立方米，比上月（2021年12月）增加了9.9-9.67=0.23亿立方米>0.2亿立方米，答案选a。

132.2020年，中石化供气量占c市天然气用量的比重比上年：
　　a．减少了不到3个百分点　　b．增加了不到3个百分点
　　c．减少了3个百分点以上　　d．增加了3个百分点以上

【答案】b。解析：比例的变化分析与差值计算。由材料知，2020年,c市天然气用量为107.47亿立方米,同比增长3.83%。其中，中石化供应33.51亿立方米,同比增长8.8%。中石化增长率b=8.8%>c市总用量增长率a=3.83%，故占比比上年增加，排除a、c。增加的百分点为：

，答案选b。

133.2019—2020年，c市cng用气总量约为多少亿立方米：
　　a．15　　b．17　　c．11　　d．13

【答案】a。解析：基期量计算。由材料知，2020年,c市天然气用量为107.47亿立方米,同比增长3.83%。其中,cng用气6.99亿立方米,同比下降13.92%；故2019年c市cnc用气总量为6.99/(1-13.92%)≈6.99/0.86=8.13亿立方米，故2019—2020年，c市cng用气总量约8.13+6.99=15.12立方米，与a项最接近，答案选a。

134.以下哪个饼图最能准确反映2021年1—2月c市天然气用量中，民用气（白色）、cng用气（黑色）和工业用气（斜线）的占比关系：

< p>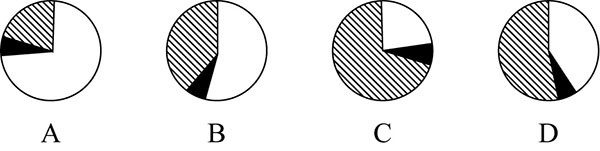

【答案】d。解析：比例与圆形图分析。三个用气量同属一个总体，占比大小与用气量大小成正比。由材料知，2021年1—2月,c市天然气用量为19.21亿立方米,其中，民用气为7.78亿立方米,;cng用气1.14亿立方米,；工业用气10.29亿立方米。结合图形比较数据，d项符合，答案选d。
　　a．如上图所示　　b．如上图所示　　c．如上图所示　　d．如上图所示
135.以下柱状图反映了c市天然气2020年12月—2021年2月间哪一数值的变化趋势：

< p>

　　a．中石油供气量　　b．中石化供气量　　c．民用气用量　　d．工业用气用量

【答案】b。解析：条件图分析。

2020年12月 2021年2月 2021年1—2月 1月供应

中石油供应： 7.22 6.7 14.23 14.23-6.7=7.53 不合

中石化供应 2.45 2.61 4.98 4.98-2.61=2.37 符合。

民用气用量： 3.98 3.56 7.78 7.78-3.56=4.22 不合。

工业气用量： 5.05 5.23 10.29 10.29-5.23=5.06，不合。

综合上述，答案选b.

< p>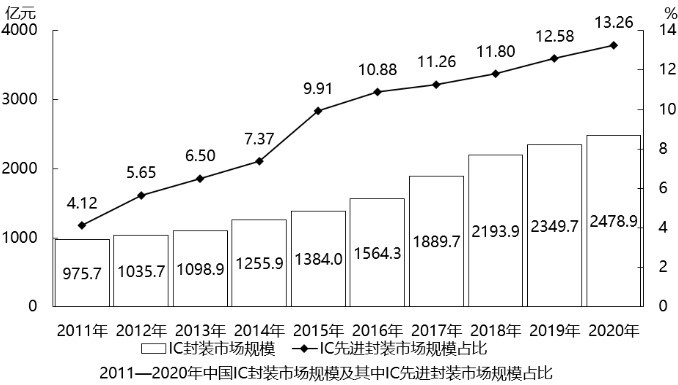

116、2019年，中国ic先进封装市场规模约为多少亿元？
　　a、296　　b、279　　c、252　　d、235

【答案】a。解析：比例计算。由图形知，2019年中国ic封装市场规模为2349.7亿元，其中先进封装市场规模占比为12.58%，则2019年中国ic先进封装市场规模约为：

2349.7×12.58%≈2350×1/8=294，与a最接近。
117、“十三五”（2016—2020）年期间，中国ic封装市场总规模：
　　a、不到1.0万亿元　　 b、在1.0—1.1万亿元之间
　　c、在1.1—1.2万亿元之间　　d、超过1.2万亿元

【答案】b。解析：简单基础计算。由统计图得，2016-2020年中国ic封装市场总规模为：

1564.3+1889.7+2193.9+2349.7+2478.9≈1560+1890+2190+2350+2480=10470=1.047万亿，在b 项范围之内。
118、2012—2020年，中国ic封装市场中ic先进封装市场规模占比同比提升1个百分点以上的年份有几个？
　　a、2　　b、3　　c、4　　d、5

【答案】a。解析：简单百分点比较。由图形知，2012-2020年中国ic先进封装市场规模占比同比提升1个百分点以上的有2012年（5.65%-4.12%=1.53）、2015年（9.91%-7.37%=2.54%），共2年，答案选a。

119、2012—2020年，中国ic封装市场规模同比增量最大的年份是：
　　a、2019年　　b、2018年　　c、2017年　　d、2016年

【答案】c。解析：增量比较。结合条形数据，粗略比较每年条形图与前一年条形图高度差值，知，2016—2019年间增量变化较大：

2016年：1564.3-1384.0=180.3； 2017年：1889.7-1564.3=325.4

2018年：2193.9-1889.7=304.2； 2019年：2349.7-2193.9=155.8亿元；比较可知，2017年同比增量最大，答案选c。

120、已知2020年中国ic封装市场规模同比增长x亿元，ic封装市场中ic先进封装市场规模占比同比增长y个百分点，而2020年往后中国ic封装市场规模及ic先进封装市场规模占比每年都分别同比增长x亿元和y个百分点，则到“十四五”最后一年（2025年），中国ic先进封装市场规模将达到多少亿元?
　　a、469　 　b、575　 　c、433　 　d、521

【答案】d。解析：年均增长量问题。由图形知，2020年、2019年ic封装市场规模分别为2478.9亿元、2349.7亿元；ic先进封装市场规模占比分别为13.26%、12.58%。则x=2478.9-2349.7=129.2亿元；y=13.26%-12.58%=0.68%,即0.68个百分点。根据年均增长规律，2025年ic封装市场规模=2478.9+129.2×5=3124.9亿元，ic先进封装市场规模占比13.26%+0.68%×5=16.66%≈3125×1/6=521亿元。答案选d。

< p>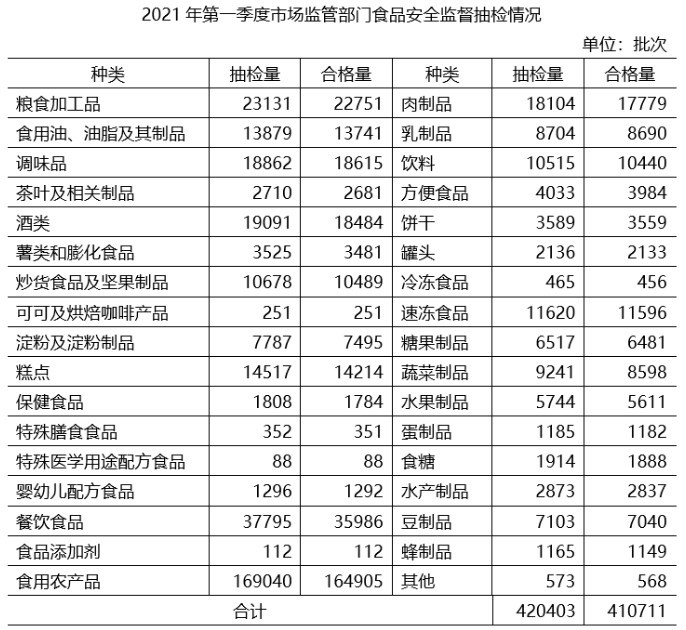

121、表中所列食品类别中，2021年第一季度所有抽检样本全部合格的有几类？
　　a、2　　b、3　　c、4　　d、5

【答案】b。解析：简单信息查找比较题。比较表格数据可得，全部合格的有3类：可可及焙烤咖啡产品、特殊医学用途配方食品、食品添加剂。
122、2021年第一季度市场监管部门食品安全监督抽检的总体不合格率在以下哪个范围内？
　　a、不到1%　　b、1%—2％之间　　c、2％—3％之间　　d、3％以上

【答案】c。解析：比例计算。根据表格最后合计数据可得，不合格率为：

，答案选c。

123、2021年第一季度市场监管部门食品安全监督抽检量最多的3个食品类别，同期抽检不合格量约是其余所有类别抽检不合格量的多少倍？
　　a、0.5　　b、0.8　　c、1.3　　d、1.9

【答案】d。解析：倍数计算。比较表格数据知，抽检量最多的3个食品类分别是食用农产品169040、餐饮食品37795、粮食加工品23131，这3类产品的不合格量为：食用农产品：169040-164905=4135，餐饮食品=37795-35986=1809，粮食加工品=23131-22751=380，这3类产品不合格总量为4135+1809+380=6324，同期抽检的所有食品不合格量=420403-410711=9692，则倍数为：

倍，答案选d。

124、将①肉制品、②乳制品和③蛋制品按2021年第一季度市场监管部门食品安全监督抽检合格率从高到低排列，以下正确的是：
　　a、③②①　　b、②③①　　c、①②③　　d、①③②

【答案】b。解析：比例计算比较。根据表格数据计算比较合格率：

①肉制品抽检合格率：

；

②乳制品抽检合格率：

；

③蛋制品抽检合格率：

;三者从高到低排列为②③①。答案为b。

125、关于2021年第一季度市场监管部门食品安全监督情况，以下信息能够从上述资料中推出的有几项？
　　①蔬菜、水果制品的总体抽检合格率高于95%
　　②样品抽检量超过1万批次的食品类别有12个
　　③糕点类食品的抽检合格量是不合格量的50倍以上
　　a、0项　　b、1项　　c、2项　　d、3项
【答案】a。解析：综合分析题。

①根据表格知，蔬菜制品抽检量为9241，合格量为8598；水果制品的抽检量为5744，合格量为5611，则（9241+5744）×95%=14235.75>8598+5611=14209，即蔬菜、水果制品的总体抽检合格率低于95%，错误。

②比较表格各类产品的抽检量，样品抽检量超过1万批次的食品类别共有11个，错误。

③表格知，糕点食品的抽检量为14517，合格量为14214，则抽检不合格量为：14517-14214=303，而14214<303×50=15150，即糕点食品的抽检合格量不到不合格量的50倍，错误。

综合上述，答案选a。

2022年国考资料分析：

历年来国考资料分析整体难度最简单的一次。只有个别综合分析题。有多个简单信息查找题、图形分析判断题，简单计算、比较题。考的知识点也是常规考点，主要有：比例计算、比较；基期量计算；比较的变化分析；比例的变化与差值计算；倍数计算；增长量的计算、比较大小；平均数计算等知识点。